|
Question 2. Parsing strategies
(a) From Question 1 above, it can be clearly seen that the parser, when given the choice
to reduce or shift, always decides to reduce, without any further considerations. This
happens at both Step 14 and Step 23, which have been identified as the points where the parser resolves shift-reduce conflicts
incorrectly, in turn leading to dead-ends. Therefore, the parser is automatically
using the reduce > shift strategy.
(b) Whether or not a single strategy can work for the example
sentence in Question 1 is somewhat dependent upon the definition of “single.”
Suppose “single” means
only one of either the shift > reduce or the reduce > shift strategies. Then
assume that the shift > reduce strategy is implemented. The parser will first
begin by shifting all of the words of the sentence. Once the last word is shifted,
the parser will start reducing, since no more words are left to shift. Since
what is currently on the top of the stack is the last word “statue,” this word is reduced to being indicated as a Noun (N). As
there continues to be nothing to shift, the parser will try to reduce again, but instead reaches a dead-end. This is because the previously reduced N cannot be reduced any further without its adjacent neighbors not
having been reduced to parts of speech. This dead-end is captured in the following
snapshot:

Thus the shift > reduce strategy alone cannot work for the example sentence in Question 1. As for the reduce > shift strategy, it has already been discussed in Question 1 and Part (a) above that
it alone also cannot work, getting stuck at Step 14 and Step 23. But the wrong
reductions performed at both of those steps were due to the parser putting together NP and VP to form S, so if this action
can be ignored (i.e. assumed that it is postponed until the very end), the reduce > shift strategy will work.
That leads to the second definition; if “single” is to mean any particularly defined strategy implementing a combination of the shift > reduce and
the reduce > shift strategies, a successful working strategy, which utilizes reduce > shift except when the reduction
to be performed is [S à NP VP], can be formulated
to work.
(c) The shift > reduce strategy will produce a bushy (flatter rather
than deeper) shape in its parse tree, and an example of this is the snapshot provided above in Part (b). Meanwhile, the reduce > shift strategy will produce a straggly (branching down to the right or left)
shape in its parse tree, relative to the shift > reduce strategy, and examples of this are the snapshots provided above
in Question 1.
(d) The reduce > shift strategy has the effect of minimizing
the number of elements on the stack (or the stack depth), since it reduces terminals to non-terminals as they are shifted
over, which are then further reduced, whenever possible, into fewer non-terminals. This
in turn results in a reduction in the number of individual elements that need to be kept track of using the stack, as is apparent
from the very definition of the word “reduce.”
(e) People certainly do seem to have definite preferences
in the way they construct parse trees for sentences that they encounter. I believe
that such preferences differ among individuals, and may conform to neither the shift > reduce nor the reduce > shift
strategy; for instance, the way I would parse the sentence “my dog saw a man in the
park with a statue on the grass behind the fence” is as shown below, where (1) the man is in the
park, (2) that man is holding a statue, (3) that man is on the grass, (4) the grass is behind the fence, and (5) my dog is
the one that saw (1) through (4):
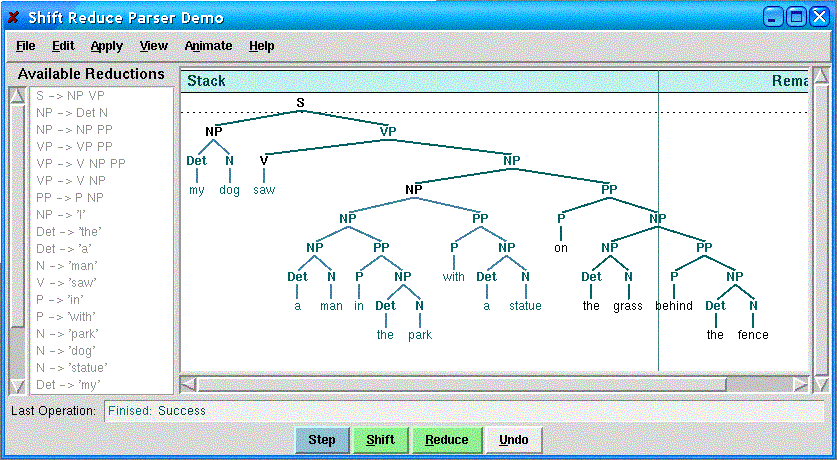
It may be very likely that an individual’s parse tree depends
heavily on what his first language is, or even just on what language’s mode he
is in when he hears the English example sentence given in this part. From personal
experience, immediately after I switch back to speaking English after speaking Japanese with my mother, I often jumble up
the words in my speech and become a bit slow in responding to others talking to me in English, despite the fact that English
is one of my first languages.
Question 3. Reduce-reduce conflicts
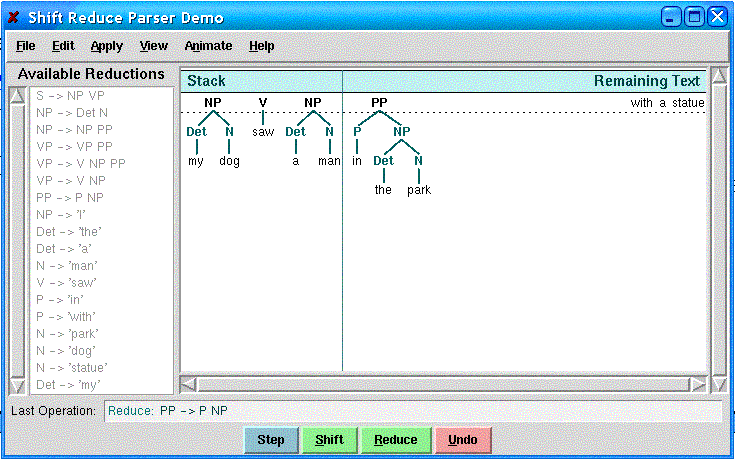
(a) The current srparser grammar has a reduce-reduce conflict;
when a situation occurs where non-terminals line up as V NP PP, and if a reduction is called to take action next, the parser
must decide whether to reduce just the NP and PP to NP (according to [NP à
NP PP]) or reduce all of V, NP, and PP to VP (according to [VP à
V NP PP]). The following snapshot shows such a situation:
The reduce-reduce conflict does not surface when using strictly the reduce > shift strategy, the
shift > reduce strategy, or the “reduce > shift except when [S à NP VP]” strategy on the example sentence given in Question
1, since NP and PP do not line up in that particular order, let alone being to the right of a V.
(b) A possible strategy to resolve the reduce-reduce conflict
explained in Part (a) would be to reduce first the smallest group of reducible non-terminals, which, in this case, would be
to abide by [NP à NP PP]. This
strategy is a sensible one in light of the idea that the PP would most likely reside next to the phrase (in this case, NP)
that it is directly modifying. Even at a more general level, it would not be
insensible to assume that, in English, a phrase that modifies another phrase often resides close to the latter. The simplest way to implement this into the parser would be to first order the grammar’s available reductions in the order reflecting this strategy, then simply program the parser to abide
by the reduction that is higher in the order listed, whenever there is a conflict. Such
implementation design is already in use by the parser, as is specified in the “Instructions” file under the “Help” tab
of the parser window.
Question 4. Stack depth and time complexity
(a) If we measure sentences in terms of n, their length
in number of words, then as n grows without bound, the stack of the shift-reduce parser can grow deep with order O(n). An example of such a situation would be the case where the parser is made to parse
a sentence that has the following structure: NP V NP PP PP PP …… PP. If each of the PP modifies the PP directly to its left, then as the length of the
sentence (which can also be estimated by the number of PPs, or more explicitly, a constant multiple of the number of PPs)
grows, the depth of the resulting structure would also grow proportionally. The
following snapshot shows such a case (for the purpose of illustration, I closely imitated the sample sentence from the laboratory
handout that ignores meaning):

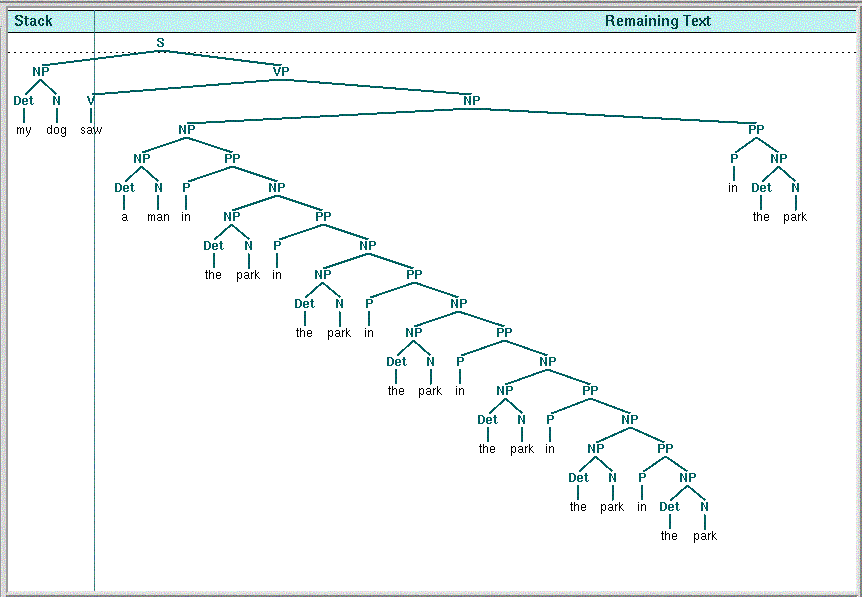
(b) The srparser is not real-time, since the time between
the shifts can last arbitrarily long, depending on the sentence structure. The
best way to explain this would be through an example; suppose that we take the sample sentence from Part (a), but add another
PP (“in the park”) at the end, which modifies not only the PP
directly preceding it, but rather the entire part of the sentence following the V. Then,
before the words from the last PP can get shifted, that entire part being modified must be reduced. The following snapshot illustrates this case:
Judging from the fact that the srparser is not real-time, as human sentence processing arguably is, the srparser does
not seem to be fit to really serve as a model of human sentence processing.
(c) The first step to finding the recurrence relation would be to start
off by finding the initial conditions of the recurrence (or the basis of the recursive definition):
P1: (x) à 1 way to partition
P2: (xx) à 1 way to partition
P3: (xxx) (x(xx)) ((xx)x)
à 3 ways to partition
P4: (xxxx) (x(xxx)) (xx(xx)) ((xxx)x) ((xx)xx) ((xx)(xx)) (x(xx)x) à 7 ways to partition
P5: (xxxxx) (x(xxxx)) ((xxxx)x) (xx(xxx)) (x(xxx)x) ((xxx)xx)
(xxx(xx))
(xx(xx)x) (x(xx)xx) ((xx)xxx)
(x(xx)(xx)) ((xx)x(xx))
((xx)(xx)x)) ((xx)(xxx)) ((xxx)(xx)) à 15
ways to partition
From these, the recurrence relation can be found
to be
P1 = 1
P2 = 1
Pn = 2Pn-1 + 1 , n > 2
The closed form solution for n > 2 (and also
for n = 2), derived from the recurrence relation, is
Pn = 2n-1 – 1
Chart Parsing
Question 5
The top-down and the bottom-up strategies both
reach the same two parses, though through constructing a different number of different edges.
For the sample sentence, the top-down strategy constructs 77 edges, whereas the bottom-up strategy constructs only
54, which is approximately 30% less than the number of edges created by its top-down counterpart.
The main difference in the types edges created by the two distinct
approaches lies in the fact that the top-down strategy creates many more partial edges; while the number of complete edges
for both cases are equal at 19, the top-down approach creates 58 partial edges, as opposed to the 35 partial edges created
by the bottom-up approach. This is due to the fact that the top-down approach,
when starting with the partial edge for the broadest possible parsing ([S à
* NP VP]), further creates all possible parsing for the first constituent to the right of the dot on the right side (NP in
this case), and continues to do so recursively until the partial edges created are those of individual words in the grammar
(e.g. the recursion of creating all possible partial edges in this first state would end when all the partial edges for the
Det words in the grammar have been created, since one of the ways in which NP is parsed is [NP à
Det N]). On the other hand, since the bottom-up strategy only creates partial
edges for the words that are present in the input sentence, then builds further edges up from there, it can avoid creating
many of the partial edges that the top-down approach needs to create.
I think that the bottom-up strategy being more
efficient over the top-down strategy will generally hold, unless the number of rules (including the ones that indicate individual
words) is decreased to a point where there may not exist any ambiguities. For
instance, if there were to be only one way to parse S, one way to parse NP, one Det, and so forth, then the top-down approach
would only create partial edges that will eventually succeed into becoming complete edges, and in turn not be relatively inefficient.
Question 6
Each of the parsing strategies creates edges that
the other one does not. The following are snapshots of both strategies with their
unique edges indicated by sky blue squares:
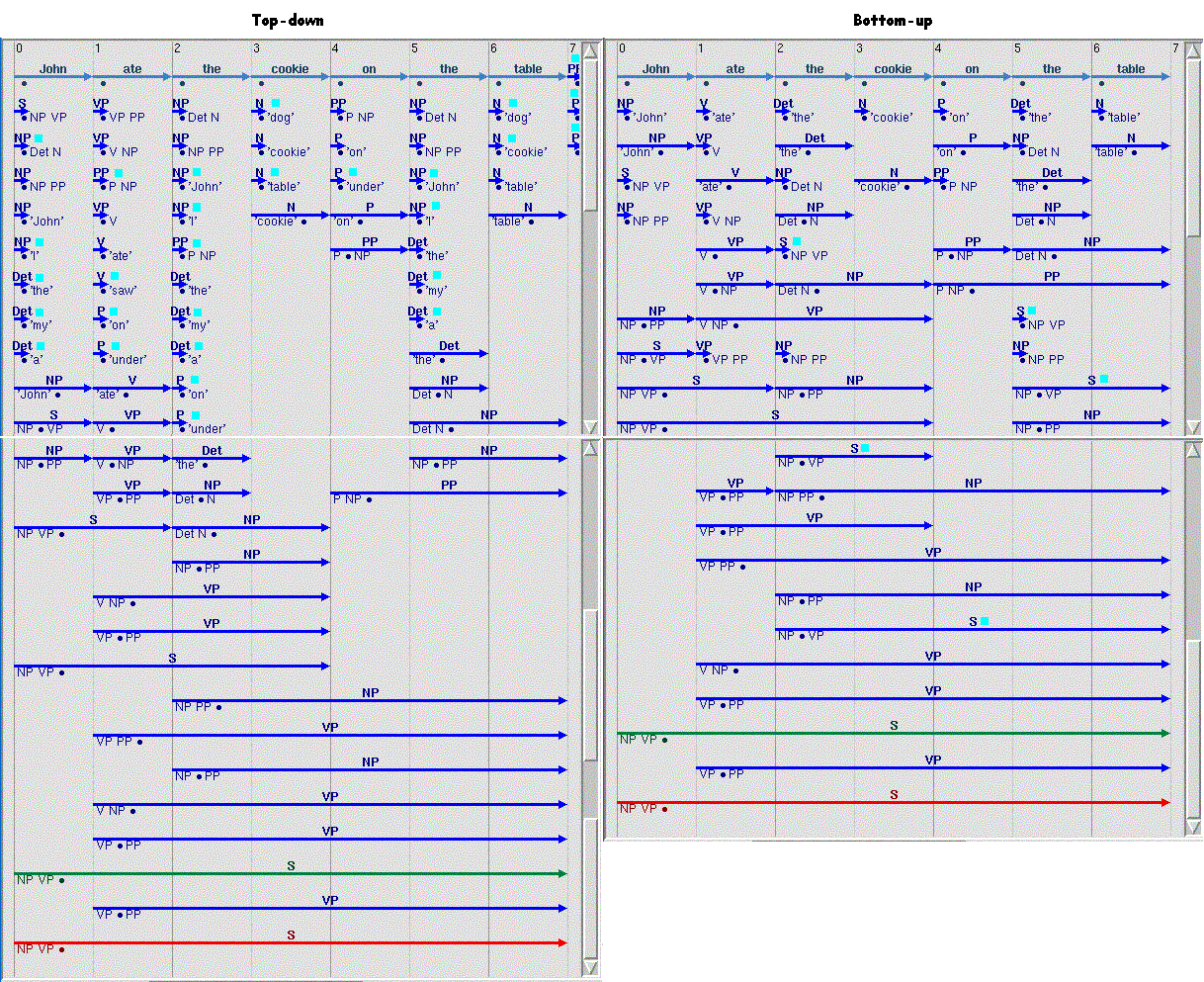
An example of edges created by the bottom-up strategy, but not
by the top-down strategy, are edges of the kind [S à NP VP] that do not stem from
the beginning of the sentence. The bottom-up strategy creates these because,
whenever it creates a complete edge for a part of speech, say, NP, it creates the partial edges for all the grammar rules
that have right sides that begin with that part of speech, such as [S à NP VP], regardless of where
in the sentence that part of speech is. The top-down strategy does not create
these edges, since they create edges that begin with parts of speech that exist on the right sides of already created partial
edges, and S is not on any grammar rule’s right side.
The top-down strategy also creates edges that the
bottom-up strategy does not. As is described extensively in Question 5 above,
the top-down approach creates all possible parsing for the first constituent to the right of the dot on the right side of
previously created partial edges. The bottom-up strategy, as is also described
in Question 5, does not create some of these partial edges, since it initializes
by only creating partial edges for the words that are present in the input sentence, then builds further edges up from there.
Question 7
By precisely controlling the parser, I was able
to find a combination of top-down and bottom-up strategies that is more efficient (i.e. produces fewer edges), although only
slightly, than both the pure top-down and the pure bottom-up methods. I started
by attempting to figure out the minimum number of distinct edges required to describe both parse trees, by looking at the
snapshot of the bottom-up parsing (since it creates the fewer of the two pure strategies); I counted as necessary all the
edges that either are or lead to complete edges. The following snapshot of the
completed bottom-up parsing has pink checkmarks on all the ones I counted as necessary, and green marks on all the ones I
counted as unnecessary:

I thus estimated the number of absolutely necessary edges to
be 37. I then checked which of the unnecessary edges created by the bottom-up
strategy do not exist in the top-down parsing; it turned out that the extra edges of the kind [S à
NP VP] (marked in yellow above), as explained in Question 6 above, were not created by the top-down parsing. As a result of this finding, I decided to target the elimination of these edges in my combined strategy,
in order to find a method that creates the two complete parse trees with fewer total edges.
The combined strategy decides which action to take
by the following steps/guidelines:
1) Initialize using Bottom-Up Initialization Rule (Bi), since that
creates the partial edges for every word in the input, making it not necessary for the top-down strategy to create partial
edges for all words included in the grammar.
2) Continue with Bottom-Up Strategy (b), until an edge with the
dot at the beginning of the right side is created.
3) If the created edge is [S à
* NP VP] that is not at the beginning of the sentence, repeat Step 2. If not,
continue on to Step 4.
4) Use the Top-Down Strategy (t), until either the edge created
at the end of Step 2 is completed, or an edge of the kind [S à NP VP] (that is not at the beginning
of the sentence) is created. If the two parse trees have not been both created,
go back to Step 2.
This produces 52 edges, 2 edges less than the pure bottom-up
strategy. The edges not created are of the unnecessary 5 targeted, since when
[S à * NP VP] is created other than at the beginning of the sentence,
it is not allowed to continue onto create [S à NP * VP]. The following are snapshots of the final chart and the actual edges, respectively, which result from
using this combined strategy to parse:

Earley Parsing
Question 8. Earley parsing efficiency
Earley parsing in fact achieves the goal of reducing
the number of edges constructed from those of the pure top-down and the pure bottom-up strategies; it produces 52 edges for
the parse of “John ate the cookie on the table,” which is less than both the 77 produced
by the top-down strategy and the 54 produced by the bottom-up strategy. Thus,
in the case of our sample sentence, Earley parser is the best. (Although the
question asks to parse “I saw my dog with a cookie,” judging from the words specified in the grammar of the lab3a.grm
file and also for accurate comparison against other parsing methods discussed earlier, I parsed “John ate the cookie on the table,” the sample sentence used in
all other parts of this lab, for answering this question.)
Question 9. Earley parsing and ambiguity
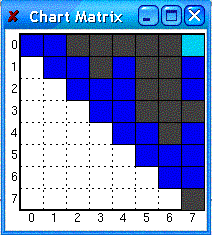
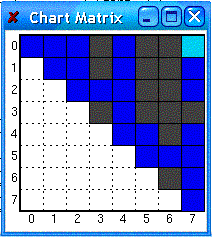
The chart, which is of quadratic size, is not actually
being packed with a possibly superpolynomial number of distinct trees. It is
in fact merely a representation of which states (noted by the row/column number of the chart (matrix)) are being connected
due to the edge currently being created. Thus, even if more than one edge connects
the same states together, and in turn occupies the same chart position, the position has no worry of overflowing in capacity.
Then what keeps track of the distinct parsed trees? The tree structures are actually in the edges themselves; each non-terminal representation of an edge,
along with the dot position, encodes the return position/pointer that guides the branching of each tree. For a clearer picture of what is happening, take a look at the following record of edge constructions,
which is the log from the parsing performed in Question 8:

Since the edge marked by the purple square is complete, it signals
that the edge preceding that would have been a partial edge with the dot placed between the two non-terminals on the right
side. Such an edge is marked by the pink square, and this indicates where the
division in the sentence occurs between the NP and the VP, available from the log through the “|[--> . . . . . .|” printed with this edge. The two edges marked by blue squares both adhere to the information found, and thus
indicates the need for two separate trees. The pointing process continues down
each tree in a similar manner. Also, with regards to the chart serving as a representation
of state relationships, notice that, although the two edges marked by blue squares occupy the same chart matrix position (shown
by the identical “|. [-----------------]|” printed with them both), this
is not explicitly expressed in any way by the chart itself, shown below:
|

